Note: this article uses MathJax to display formulas written in TeX. Please enable Javascript in order to see the formulas correctly.

One week has passed since the end of LSE Week 2012 and I have received several partial solutions for the crackme that was released at the start of LSE Week for people to play with. Most people who bothered writing partial solutions were able to break the packing and anti debugging parts of it, but stopped at the very end when they faced a simple hashing algorithm they had to reverse to generate a valid key for the crackme. In pseudocode, the algorithm was the following:

a, b, c, d are the four 32 bits integers given as input (key)

Compute a simple checksum in order to avoid having several good solutions
to the problem:
    if ((ROTL((a ^ b) - (c ^ d), 17) ^ (a + b + c + d)) != 0xa6779036)
        return 0;

Kind of useless step just to make things a bit harder
a = a XOR c
b = b XOR d

Then, 128 times in a row, for each integer:
    Shuffle the bits of the number (using a predefined table)
    XOR the number with a predefined constant
    Rotate left the number by N bits (N being another constant)

Check if:
    a == 0x8e2c4c74
    b == 0xa6c27e2a
    c == 0xf5e15d3d
    d == 0x7bebc2ba

Clever people might notice that all of the operations done by that “hashing” algorithm are actually non destructive and completely reversible. That means our hashing function is bijective (no collisions) and that it is very easy to get the input from the output: just run it in reverse (rotate left becomes rotate right, XOR stays the same, shuffle uses a slightly modified table). It was meant to keep the crackme easy to crack once the code has been recovered and understood. Unfortunately, some last minute bugs cropped up in the implementation of the algorithm (never try to fix bugs at 4AM without automated tests…) and made the algorithm completely different:

a, b, c, d are the four 32 bits integers given as input (key)

Compute a simple checksum in order to avoid having several good solutions
to the problem:
    if ((ROTL((a ^ b) - (c ^ d), 17) ^ (a + b + c + d)) != 0xa6779036)
        return 0;

a = a XOR c
b = b XOR d

Then, 128 times in a row, for each integer:
    Shuffle the bits of the number using a table that might map some bits
    two times, and some other bits zero times (DESTRUCTIVE)

    XOR the number with a predefined constant
    Rotate left the number by N bits (N being another constant), except if
    this is the last number - in this case, rotate the third integer and
    use it as the new value for the last integer

Check if:
    a == 0x8e2c4c74
    b == 0xa6c27e2a
    c == 0xf5e15d3d
    d == 0x7bebc2ba

The first error (in the shuffling part) comes from an indexing error in my bits position table. The table was defined like this:

// Maps the input bit position to the output bit position
static const char mapping[128] = {
    // First integer
    2, 14, 4, 24, 7, 31, 16, 18, 30, 17, 12, 27, 6, 26, 9, 22,
    1, 28, 5, 3, 11, 23, 13, 25, 19, 20, 10, 29, 8, 15, 21, 0,

    // Second integer
    26, 20, 15, 27, 28, 14, 21, 7, 17, 22, 31, 12, 4, 13, 8, 10,
    23, 19, 18, 25, 9, 2, 5, 11, 6, 3, 24, 1, 0, 30, 29, 16,

    // Third integer
    4, 26, 20, 13, 21, 29, 3, 14, 5, 22, 18, 6, 28, 23, 16, 10,
    15, 27, 25, 1, 17, 0, 30, 2, 8, 24, 7, 9, 31, 19, 12, 11,

    // Fourth integer
    8, 22, 26, 1, 20, 2, 30, 23, 6, 9, 0, 14, 18, 31, 3, 21, 4,
    29, 24, 7, 12, 28, 16, 25, 11, 17, 19, 27, 5, 10, 15, 13
};

But the indexing was done like this:

// *pn points to the current integer, i is the index of this integer (0, 1,
// 2 or 3), j is the current bit.
newn |= ((*pn >> scramble[(i << 2) + j]) & 1) << j;

That i << 2 should actually be a i << 5 in order to use the whole mapping table. This bug makes the algorithm destructive because some bits from the input will not be used to generate the output. That means you can’t get the input of the step from its output: the destroyed bits could have been 0 or 1.

The second bug is actually a stupid typo:

a = ROTL(a, 7);
b = ROTL(b, 13);
c = ROTL(c, 17);
d = ROTL(c, 25);

I don’t think this requires much explanation.

Now that the context of this article has been explained, the real question for me was the following: do these errors make the crackme unsolvable or can it still be solved easily using either bruteforce or more complex analysis techniques?

SAT and its applications to cryptography

I started writing a bruteforcer for this hash using backtracking for each destroyed bit and only exploring the branches that would be valid later on by predicting as much as possible. Unfortunately, while that worked for a small number of iterations of the hash, the original algorithm used 128 iterations and the number of possible combinations increased a lot too fast to use such a simple technique.

Two days later I got reminded by a friend of a talk presented by Mate Soos at Hackito Ergo Sum 2011 about SAT solvers and their application to cryptography for breaking weak ciphers and hashes. Mate is the author of CryptoMiniSat, a very fast implementation of SAT with a few tweaks that can be used to increase efficiency for crypto usages.

Before going into the details of how to use SAT to break ciphers, let’s talk a little bit about SAT solvers. SAT solvers are programs designed to solve the Boolean Satisfiability Problem, which can be expressed very simply like this: For this boolean formula, can I find values for the variables that make the formula true. This is an NP-complete problem (which means you can’t solve the general case of that problem in polynomial time, only exponential time or slower) and is actually kind of the canonical NP-complete problem: it is a very common technique to reduce a problem to show that it is equivalent to SAT in order to prove that it is an NP complete problem.

Most SAT solvers take their input in a format called DIMACS, which is an easy-to-parse representation of boolean formulas in CNF (Conjunctive Normal Form). A CNF formula is a special case of boolean formula which is always written like this:

$$(X_i \vee \neg X_j) \wedge (\neg X_k \vee X_l \vee \neg X_m \vee X_n) \wedge \ldots$$

Basically, CNF is a logical product (aka. conjunction) of sums of variables or negated variables (\(\neg A\)). Every boolean formula can be converted into an equivalent CNF formula, either manually (distribute the \(\vee\) over products) or through an automated process (there are some conversion tables between simple boolean equations and their CNF equivalent).

SAT solvers have a lot of applications and tend to be very optimized in order to have extremely good performances in most cases. It is common to try to solve SAT problems with several hundreds of thousands of clauses (a clause is a single sum of variable, like \(A \vee B \vee \neg C \vee D\)) and tens of thousands of variables.

In his talk last year, Mate Soos told us about how HiTag2 (a cryptosystem used in car locks) was reverse engineered, then translated to mathematical formulas and finally converted to CNF formulas describing the relations between input bits and output bits. If you are interested by that talk, it is available on Youtube. I thought that this technique might be of some use in breaking my hash algorithm and started translating the hash algorithm to an equivalent CNF representation.

Breaking the hash with SAT

First of all, the definition of the algorithm would most likely use several thousands of clauses and about as much variables, so writing it by hand is out of the question. I started by writing a very simple library to generate DIMACS files, which exposes the following Python API:

  • CNFGenerator.new_var() generates a new SAT variable instance, which has only one operation: logical negation (written -x)
  • CNFGenerator.add(v1, v2, ..., vN) adds a clause to the output DIMACS file
  • CNFGenerator.output() outputs the DIMACS representation

CryptoMiniSAT also provides a very useful extension to DIMACS for cryptographical uses: the ability to use XOR clauses which are \(A \oplus B \oplus C \oplus \ldots\). These prove very useful in order to write equivalences (\(A \Leftrightarrow B \equiv \neg (A \oplus B) \equiv \neg A \oplus B\)) or simply XOR relations. CNFGenerator.add_xor handles the generation of such clauses.

Let’s start by defining our input variables. They are four vectors of 32 bits, so 128 boolean variables:

def cnf_int(gen, bits):
    return [gen.new_var() for i in range(bits)]

# Input variables
a = cnf_int(gen, 32)
b = cnf_int(gen, 32)
c = cnf_int(gen, 32)
d = cnf_int(gen, 32)

If you follow the pseudocode above, the next step would normally be the checksum. This is actually the hardest part of this algorithm to formalize because of the arithmetic operations (additions and substractions of 32 bits numbers). We’ll do that last. The following step is a ^= c; b ^= d. This is quite easy to formalize. Let’s do it for the general case , i.e. a = b ^ c. What this does is “make each bit of a equal to the same bit of b XOR the same bit of c”. To formalize it, we can introduce a new variable \(A\) which is equivalent to \(B \oplus C\), which means the clause can only be true iff \(A\) has the same value as \(B \oplus C\). We just need to write that in a form that CryptoMiniSat can understand:

$$\begin{aligned} A \Leftrightarrow (B \oplus C) & \equiv \neg (A \oplus (B \oplus C)) \\\\ & \equiv \neg (A \oplus B \oplus C) \\\\ & \equiv \neg A \oplus B \oplus C \end{aligned}$$

Applied to the 32 bits of the variables and converted to Python, this gives us the following code:

def cnf_xor(gen, a, b):
    out = [gen.new_var() for i in range(len(a))]
    for (a, b, o) in zip(a, b, out):
        gen.add_xor(-a, b, o)
    return out

# a ^= c, b ^= d
a = cnf_xor(gen, a, c)
b = cnf_xor(gen, b, d)

Next comes the core of the hashing algorithm: the iterated loop shuffling the bits, XOR-ing with a constant and rotating the number. The interesting part here is that shuffling and rotating bits does not require any clause or additional variables for the SAT representation of the algorithm: For example, if you have a 4 bit integer represented as the vector \(A_3 A_2 A_1 A_0\), rotating it to the left by 2 bits transforms it to the vector \(A_1 A_0 A_3 A_2\). You just need to swap the elements in the list representing your variables. This gives us the following Python code:

def cnf_rotl(gen, n, b):
    """Performs a left rotation of n by b bits"""
    return n[-b:] + n[:-b]

def cnf_hash(gen, a, b, c, d):
    """Hashes a, b, c, d, returns new a, new b, new c, new d"""
    out = []
    for i, n in enumerate((a, b, c, d)):
        scrambled = [n[SCRAMBLE_TABLE[i][j]] for j in range(len(n))]
        xored = cnf_xor_const(gen, scrambled, XOR_TABLE[i])
        out.append(xored)

    out[0] = cnf_rotl(gen, out[0], ROT_TABLE[0])
    out[1] = cnf_rotl(gen, out[1], ROT_TABLE[1])
    out[2] = cnf_rotl(gen, out[2], ROT_TABLE[2])
    out[3] = cnf_rotl(gen, out[2], ROT_TABLE[3])

    return out

# Iterate the hash 128 times for a, b, c and d
for i in range(128):
    a, b, c, d = cnf_hash(gen, a, b, c, d)

cnf_xor_const works the same as cnf_xor but “optimized” in order to XOR with a constant number instead of a variable number.

Now that we computed the hashed values, we just need to put some clauses to make sure they are equal to the hash we are looking for. In the crackme, the hash value was 8e2c4c74a6c27e2af5e15d3d7bebc2ba. To make sure one of our boolean vectors is equal to a constant value, we add one clause per bit of the vector which forces it to True if the corresponding bit in the constant value is 1, and False if the bit is 0:

def cnf_equal(gen, n, c):
    for i in range(len(n)):
        b = c & 1
        c >>= 1
        if b:
            gen.add(n[i])
        else:
            gen.add(-n[i])

# Check for equality
cnf_equal(gen, a, 0x8e2c4c74)
cnf_equal(gen, b, 0xa6c27e2a)
cnf_equal(gen, c, 0xf5e15d3d)
cnf_equal(gen, d, 0x7bebc2ba)

With only this code, the SAT solver will generate us values for a, b, c and d that compute to the hash we are looking for. However, we still have to defeat the checksum. Let’s look at its code again:

if ((ROTL((a ^ b) - (c ^ d), 17) ^ (a + b + c + d)) != 0xa6779036)
    return 0;

We already now how to compute XORs, rotations and how to check for number equality, so the remaining part is additions and substractions on 32 bit numbers. As you may already know, substraction is actually very easy to implement in terms of addition and two’s complement, which is itself very easy to implement in terms of binary inversion and addition:

$$x - y \equiv x + COMPL2(y) \equiv x + INVERT(y) + 1$$
def cnf_invert(gen, n):
    inv = [gen.new_var() for b in n]
    for (b, i) in zip(n, inv):
        gen.add(b, i)
        gen.add(-b, -i)
    return inv

def cnf_sub(gen, a, b):
    invb = cnf_invert(gen, b)
    complb = cnf_add(gen, invb, cnf_const32(gen, 1))
    return cnf_add(gen, a, complb)

Addition on 32 bit integers is however a lot harder to define. If you did a bit of electrical engineering or if you have implemented an ALU (in HDL, with wires and logic gates, or even in Minecraft) you may know a very common way to define addition using two half adders to make a 1 bit full adder. Here is what a full adder looks like (image courtesy of Wikipedia):

Full adder

It takes two bits, A and B, as well as a carry from a previous adder (Cin), and outputs the sum A + B + Cin and the carry resulting from that sum Cout. You can then chain these 1 bit full adders to make a 32 bit adder (again, image from Wikipedia):

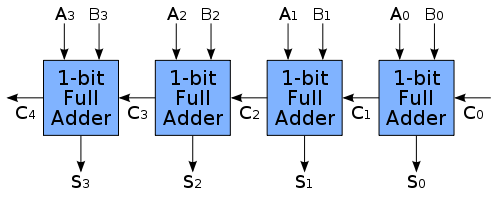
Ripple carry adder

Writing the truth table of a 1 bit full adder and simplifying the equations a bit, you get the following equations for S and Cout from A, B and Cin:

$$\begin{aligned} S & \equiv \overline{A} B \overline{C_{in}} \vee A \overline{B C_{in}} \vee A \overline{B} C_{in} \vee A B C_{in} \\\\ C_{out} & \equiv A B \vee A C_{in} \vee B C_{in} \end{aligned}$$

You can then translate these formulas to CNF to describe a 1 bit full adder for the SAT solver. However doing that manually is a lot of work (especially if you’re like me and never had proper formation on CNF and how to convert formulas to that form), so we’re just going to use the boolean algebra package from Sage to do it automatically:

sage: import sage.logic.propcalc as propcalc                      
sage: f = propcalc.formula("d <-> (~a&b&~c | a&~b&~c | ~a&~b&c | a&b&c)")
sage: f.convert_cnf_table()
sage: f
(d|a|b|~c)&(d|a|~b|c)&(d|~a|b|c)&(d|~a|~b|~c)&(~d|a|b|c)&(~d|a|~b|~c)&(~d|~a|b|~c)&(~d|~a|~b|c)
sage: f = propcalc.formula("d <-> (a&b | a&c | b&c)")                    
sage: f.convert_cnf_table()                          
sage: f                                              
(d|a|~b|~c)&(d|~a|b|~c)&(d|~a|~b|c)&(d|~a|~b|~c)&(~d|a|b|c)&(~d|a|b|~c)&(~d|a|~b|c)&(~d|~a|b|c)
sage: import sage.logic.propcalc as propcalc                      
sage: f = propcalc.formula("d <-> (~a&b&~c | a&~b&~c | ~a&~b&c | a&b&c)")
sage: f.convert_cnf_table()
sage: f
(d|a|b|~c)&(d|a|~b|c)&(d|~a|b|c)&(d|~a|~b|~c)&(~d|a|b|c)&(~d|a|~b|~c)&(~d|~a|b|~c)&(~d|~a|~b|c)
sage: f = propcalc.formula("d <-> (a&b | a&c | b&c)")                    
sage: f.convert_cnf_table()                          
sage: f                                              
(d|a|~b|~c)&(d|~a|b|~c)&(d|~a|~b|c)&(d|~a|~b|~c)&(~d|a|b|c)&(~d|a|b|~c)&(~d|a|~b|c)&(~d|~a|b|c)

We can then convert the CNF clauses Sage gives us directly to Python:

def cnf_1bitadder(gen, a, b, c):
    res = gen.new_var()
    res_carry = gen.new_var()

    # (d|a|~b|~c)&(d|~a|b|~c)&(d|~a|~b|c)&(d|~a|~b|~c)&(~d|a|b|c)&(~d|a|b|~c)&(~d|a|~b|c)&(~d|~a|b|c)
    gen.add(res_carry, a, -b, -c)
    gen.add(res_carry, -a, b, -c)
    gen.add(res_carry, -a, -b, c)
    gen.add(res_carry, -a, -b, -c)
    gen.add(-res_carry, a, b, c)
    gen.add(-res_carry, a, b, -c)
    gen.add(-res_carry, a, -b, c)
    gen.add(-res_carry, -a, b, c)

    # (d|a|b|~c)&(d|a|~b|c)&(d|~a|b|c)&(d|~a|~b|~c)&(~d|a|b|c)&(~d|a|~b|~c)&(~d|~a|b|~c)&(~d|~a|~b|c)
    gen.add(res, a, b, -c)
    gen.add(res, a, -b, c)
    gen.add(res, -a, b, c)
    gen.add(res, -a, -b, -c)
    gen.add(-res, a, b, c)
    gen.add(-res, a, -b, -c)
    gen.add(-res, -a, b, -c)
    gen.add(-res, -a, -b, c)

    return res, res_carry

Probably not the nicest way to do it, but most likely one of the simplest way. We can then use that one bit adder to make a 32 bit adder:

def cnf_add(gen, a, b):
    carry = gen.new_var()
    gen.add(-carry) # The first carry is always 0

    out = []
    for (a, b) in zip(a, b):
        res, carry = cnf_1bitadder(gen, a, b, carry)
        out.append(res)

    return out

With this we can finally implement our checksum!

sum = cnf_add(gen, a, cnf_add(gen, b, cnf_add(gen, c, d)))
sub = cnf_sub(gen, cnf_xor(gen, a, b), cnf_xor(gen, c, d))
cksum = cnf_xor(gen, cnf_rotl(gen, sub, 17), sum)
cnf_equal(gen, cksum, 0xa6779036)

Running our Python program generates a DIMACS file with 17061 variables and 19365 clauses. CryptoMiniSat can find a set of values that satisfy the clauses in less than 0.05s on my Sandy Bridge based laptop. For example, a = 0xe9e708e1, b = 0xf7e4c55a, c = 0x85e77db9 and d = 0x5467bd3c pass both the checksum and the hash and are considered a valid solution.

Using Z3 to make things easier

At first I planned to stop there: I had a proof that the crackme was still doable even with that broken hash algorithm. However when I explained what I was doing, a friend of mine told me about SMT solvers. One of their characteristics is that they can work on boolean algebra, but also functions and linear combinations of integer and real variables. For example, you can use an SMT solver for this kind of problem:

$$x^2 + y^2 < 1, 2x + y > 1$$

I looked a bit at recent SMT solvers to see if it could make cracking my hash easier. I used the Z3 theorem prover from Microsoft Research, which is not open source but has Linux binaries and nice interfaces for programming languages like Python and OCaml. Z3 can work on real numbers, integers, functions but also bit vectors, and has a nice API to do so.

As expected, things are a lot easier when your solver has native support for your native problem representation (here, bit vectors and unsigned integers). The code cracking the hash using Z3 is a fair bit slower (still less than 5s) but also much shorter and easier to understand:

def rotl32(n, sa):
    return (n << sa) | LShR(n, 32 - sa)

def hash(a, b, c, d):
    out = []
    for i, n in enumerate((a, b, c, d)):
        nn = BitVecVal(0, 32)
        for j in range(32):
            nn |= (LShR(n, SCRAMBLE_TABLE[i][j]) & 1) << j
        nn ^= XOR_TABLE[i]
        out.append(nn)

    out[0] = rotl32(out[0], ROT_TABLE[0])
    out[1] = rotl32(out[1], ROT_TABLE[1])
    out[2] = rotl32(out[2], ROT_TABLE[2])
    out[3] = rotl32(out[2], ROT_TABLE[3])
    return out

if __name__ == '__main__':
    s = Solver()

    a = BitVec('a', 32)
    b = BitVec('b', 32)
    c = BitVec('c', 32)
    d = BitVec('d', 32)

    checksum = rotl32((a ^ b) - (c ^ d), 17) ^ (a + b + c + d)

    a ^= c
    b ^= d

    for i in range(128):
        a, b, c, d = hash(a, b, c, d)

    solve(checksum == 0xa6779036, a == 0x8e2c4c74, b == 0xa6c27e2a,
          c == 0xf5e15d3d, d == 0x7bebc2ba)

Here the shorter code is mostly due to the fact I did not have any nice API to use CryptoMiniSat and to translate arithmetic operations to CNF. SMT solvers do not provide that much of an edge over SAT solvers for these kind of problems: they shine a lot more as soon as you introduce functions or real numbers that can’t easily be expressed as a bit vector.

Conclusion

Sometimes when simple bruteforce does not work you have to go a bit further to reverse a hash algorithm, and using a SAT solver enables you to do just that. The problem is not always easy to formalize, especially when you start using complex operations that can’t easily be translated, but using SAT solvers for cryptography is a very interesting technique that has already proven itself a lot of times in the past, and will probably become more and more useful in the future as SAT solvers and ways to formalize hard problems (like AES) evolve.