CSAW CTF 2012: timewave-zero.pcap (net400)
< mserrano> inb4 you have to rotate and flip the pcap and get a gzip out of it
For this exercise, we are provided a pcap file containing PMU reporting
values using the Synchrophasor protocol, also known as IEEE C37.118. The first
thing is to google that, and see what we get. The most interesting result is
Wireshark wiki. Indeed we can find example files on this page. If you
download the fourth example (“C37.118_4in1PMU_TCP.pcap”) and binary diff it with
timewave-zero.pcap you see the only changing data are the timestamps of the
Synchrophasor packets. We can therefore assume that we have to work on those
values.
There are 1353 timestamps, but if we look closer, we can see that all the timestamps are between 2012-12-21 00:00:00 GMT and 2012-12-22 23:59:59 GMT except for the last one which is 1970-01-01 00:00:00 GMT a.k.a 0. Ignoring it gives us 1352 timestamps, and 1352 just happens to be a multiple of 8 (1352 = 8 * 13 * 13). That looks good for hiding 1 bit of data in each timestamp.
So now, 1-bit per timestamp. You start the guessing game with the the classical LSB. No dice… LSB after reordering the packet according to their timestamps? No dice… 0bit and 1bit encoded accordingly to the packet being late or early in a virtual packet reordering (hey, who knows…). Guess what? No dice.
Hell we even tried animating the synchrophaser before and after packet reordering to see if something would “draw” during the animation. No dice… Time to stop the guessing game and use a weapon of mass statistical destruction: the histogram! Let’s see if we find some statistical data bias.
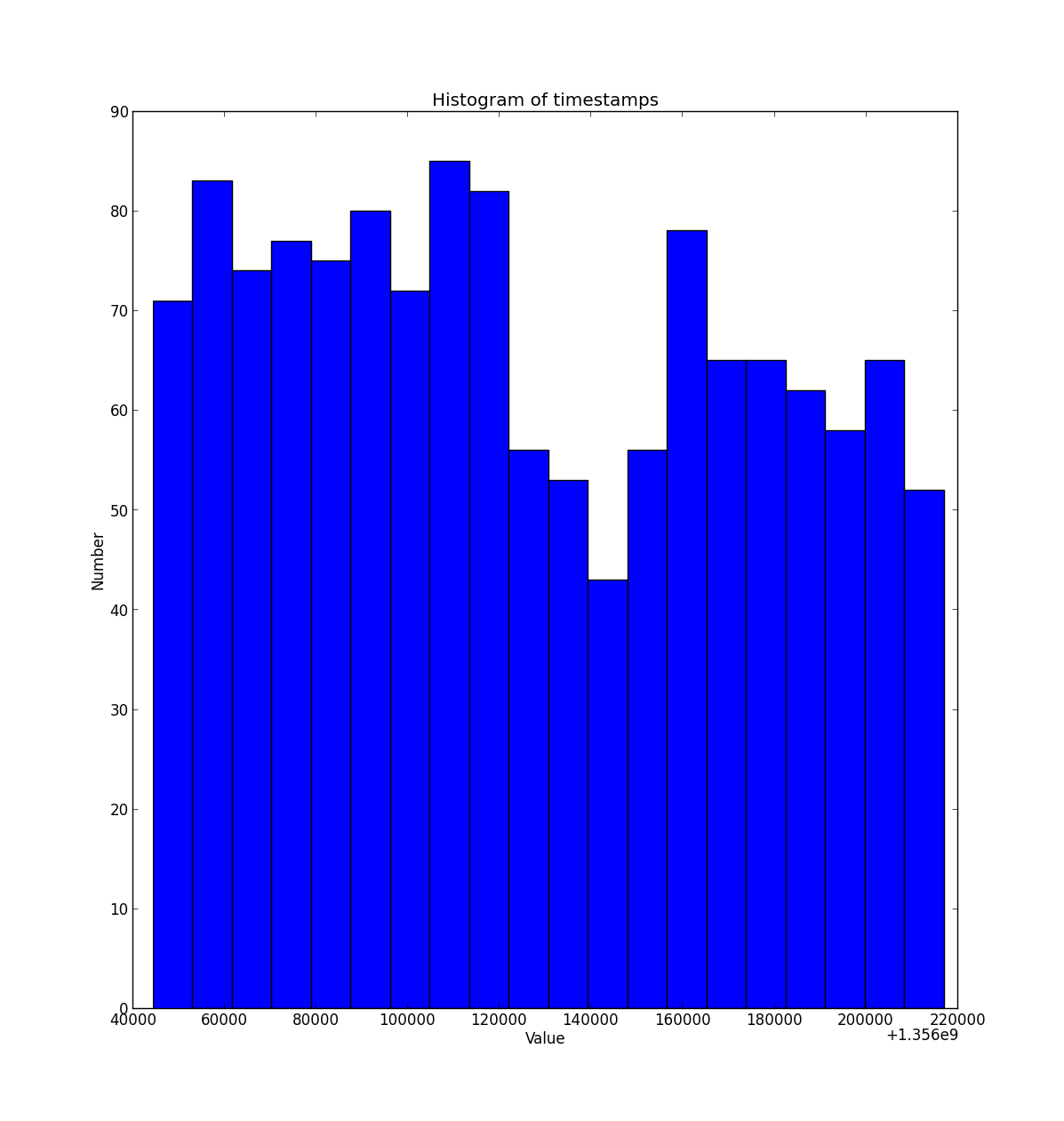
We can notice two things:
- More values on the left, which represents smaller timestamps
- A gap in the middle of the histogram
With these observation we can infer how the information are hidden in the timestamps: assuming the output should be readable ascii characters, we can assume the probability of 0-bit to be higher than of 1-bit. Looking again at the histogram, thresholding midpoint of the timestamp range would just give us exactly that. Furthermore, the gap in the middle is quite convenient insofar as it is probably preventing from ambiguities at the threshold value (should we threshold using > or >= ? )
With all this we can write a script which takes all the timestamps and get the key:
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
import sys
import struct
with open(sys.argv[1]) as f:
timestamps = [int(line) for line in f]
min_ts = min(timestamps)
max_ts = max(timestamps)
print "len = %d, min = 0x%x, max = 0x%x" % (len(timestamps), min_ts, max_ts)
out = open(sys.argv[2], "w")
val = 0
bitcnt = 0
for ts in timestamps:
if (ts - min_ts) >= (max_ts - ts):
val = (val << 1) | 1
else:
val <<= 1
bitcnt += 1
if bitcnt == 8:
out.write(struct.pack("B", val))
bitcnt = 0
val = 0
out.close()
Let’s run it:
key{411a8451f24b40647d518ccc456a9e6502f59a8992118d8bf08a65eb16feddba33561d0b383af978402631fba670b366f118505ee3c9ac3e37c9ad33b0d5db469585dd2cf5192fba9e1a99c5d336c3459089}
BUT as if steganography is not already annoyingly game-guessing enough, just submitting the key and call it a day would have been too easy, wouldn’t it? ;) We were unable to validate the key, which was refused by the web interface.
Clever ending: What if an undergradudate intern used VARCHAR(128) to store the key in the database validating the challenge? So we only pasted the 128 first chars.
Real ending:
There was something else which was different from the Wireshark wiki reference
file. One byte in the snaplen field of the global pcap header was changed
from 0xFF to 0x7F. So we thought we had to take only the
0x7F first characters (nonsense, right?). As you are well aware, 0x7F
equals 127. It sometimes helps to mistakenly copy 128 chars instead of 127 when
copy/pasting!
That’s all folks! Is timewave-zero.pcap the new BMP? Maybe not, but close enough we’d say. What do you think?